Fairness at Scale

What does it mean to be fair? I'm sure we all have a rough, hazy idea of fairness. Perhaps you think of a fair trade? Equal exchange? Justice and punishment in exchange for a crime committed? When I thought of this question, I thought of probabilities, the classic dice roll. When I roll a 6-sided dice, intuitively it is fair if I am equally likely to get any of the outcomes. Going further than this we might even reconsider the classic trolley problem. You know, 5 people tied to the left train track, 1 person tied to the right train track. A train is heading towards the left track. Should we divert the train to the right track or leave it going? Morality and value judgements aside, what if we rolled a 6-sided dice and if we got the outcomes 1-5, we save the five people, but if we roll a 6, we save the one person. Is this not the fairest outcome of the trolley problem, because we are giving each of the people the same individual chance of survival? I suppose yes, if we assume that all lives are of equal worth. But what if these systems were more complex. Let’s bring morality and value judgements back in. If we somehow decided that each of those lives were not of equal value, would it be fair to roll a dice where each side were weighted proportionally to the value of the life in question? Perhaps, and yet this would mean that someone “less valuable”, if they are tied next to someone of “greater value”, would be benefiting from proximity to that person, effectively having their chances of winning raised. On the flip side, the person of greater value is having their chance of survival lower by proximity to the “lesser” person. We see then that these people are not independent, as much as they might wish to be. The fate of the five are tied together, arbitrarily weighed against the value of the one simply by the setup of the problem itself. And this is without even asking the question: who decides who is worth more or less? This problem is of course a metaphor, read from it what you will, but now consider a more abstract example; ironically, a much more relevant example. What if I said that we want to get the biggest score we can, and with an equally weighted and fair 6-sided dice, if you roll a 6, you get another 6 rolls. If you get a 5, another 5 rolls, 4 another 4 rolls etc. Bit more tricky now. Is this fair? Every individual roll is still random, after all, and each individual roll is “fair” in terms of its outcome. Yet subsequent repeats of a “fair” trade, due to the environment in which those trades take place, can lead to profoundly unfair outcomes. Oh, I accidentally said “trade” instead of dice roll. We let’s talk economics!

Simulating an Economy

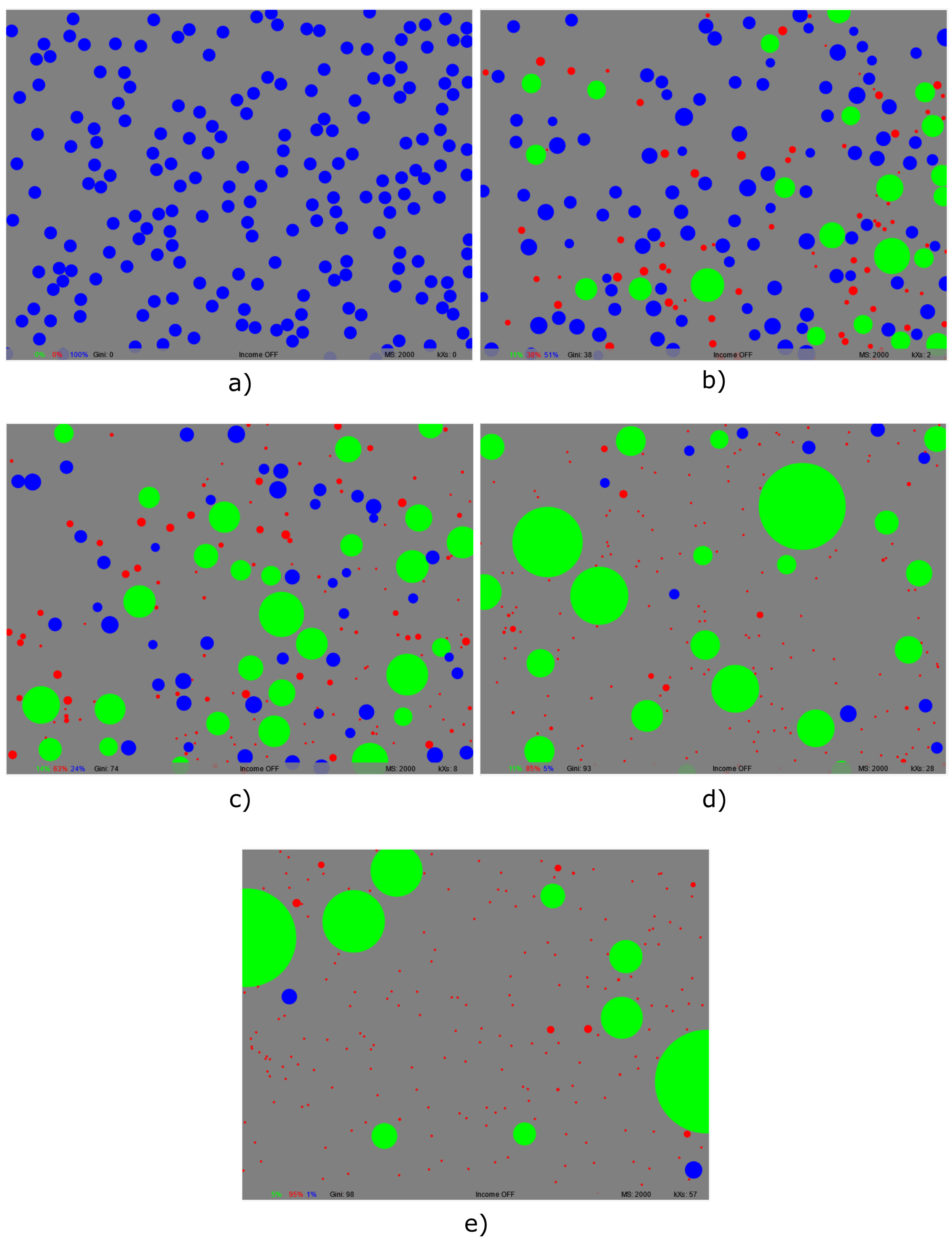
A few years ago a guy I found on the internet called Philip Rosedale (who it turns out is a big deal, look him up) had written a simulation to show how inequality emerges from a system of what we would likely consider to be fair trades. I won’t go into too much detail as he does a perfect explanation in his own blog[1], but very quickly, he imagines humans to be randomly moving objects who hold a certain amount of “value”. If they encounter another object as they’re moving around, they can exchange value with one another in a trade. Just like in our own world, for any two interacting objects, the maximum amount that can be exchanged is the total amount held by the object with the least value. So, say I have £10 (or £10 worth of stuff) and you have £100 . In that situation, the maximum amount we can exchange is £10. That seems fair, right? Surely if I try to give you my £10 and get more than £10 back in return, I’ve ripped you off. Profit, by the way, doesn’t emerge from unfair trades like this (in theory), it emerges from growth. And yet if you run a simulation of this type of trading, with a load of people moving around and trading with one another, something quite frightening occurs (see Figure 1). After a few trades some people will get a little bit of an edge. After many, many trades between many people, those same people who lucked out to start with will own the majority of everything. In fact, it can be shown that if you left this simulation running for long enough, one person would eventually own absolutely everything, slowed down only by the time it takes to actual make the trades themselves. The only reason that the other objects still exist is because the simulation was set to have a minimum value of 1 per object. If the minimum value were 0, then the giant objects would vacuum that value up as well and all the tiny red dots would…disappear. Quite harrowing. You can play with the simulation yourself here[2].

Figure 1: Trades that we understand to be “fair” lead naturally to hugely unequal distributions of wealth. The size of each circle represents its associated wealth. Time progresses from a) through to e)

Interpreting Simulations

What this simulation shows is that, given the rules of our “free” trading economy, the natural evolution of the system of trading people with no additional changes is for one person to eventually own everything. And indeed, in our very own world we can see this tendency today, and all throughout history[3]. Today, the big owners, perhaps tending towards a single owner (Elon Musk just bought Twitter), are Jeff Bezos, Warren Buffet, Mark Zuckerberg, Elon Musk, Bill Gates, and a few others of their ilk. For them too, the only thing holding them back is the time it takes them to move around and make the trades. Although our real world economic systems are more complex, the underlying mechanics and trends are roughly the same. So we may ask, if the net statistical result of “free” trades is such vast inequality, are the trades themselves really fair, and is the system itself fair? If you believe that yes, it must be a fair system because the trades themselves are fair, then I might question your self-esteem. Why would you accept such inequality, such submission to arbitrary economic power, when that power is not democratic in origin or justly earned, but simply the result of a system that allows an initial bit of luck to balloon out of control? But that’s just my opinion!

As a small side note, we might also observe that by the end of the simulation the majority of particles are tiny and red (poor), or massive and green (rich). A very small amount of the overall value is blue. What this means is that the middle (wealth) class of society is not “natural” i.e. given the rules of the system, it shouldn’t exist. The existence of a middle class is therefore a political choice, and this can be most clearly seen when politicians like Justin Trudeau of Canada talk about “growing the middle class”[4]. A conspiracy theorist might suggest that this is a very clever example of the decoy effect[5,6], intended to take the attention and heat off of the ultra-rich upper classes, but I’m not going to get into that here.

So how can this be? How can “fair” trades at the individual level, or the “microscale” (i.e. microeconomics) lead to such statistically unfair effects at the “macroscale” (i.e. macroeconomics)? The key is what we think of as “fair”. Philip Rosedale explains that because the trade is always limited by the maximum value owned by the poorer person, this statistically biases the outcome of trades towards the benefit of the richer trader. He went on to do some further investigations to alleviate this massive level of inequality: use redistributive taxes, have a universal basic income etc, but I was more interested in what set of trading rules at the microscale might lead to a more equitable macroscopic outcome. Possibly because my entire scientific background is on this very topic!

A Thermodynamic Metaphor

So I thought about compound interest and exponential growth, and I thought about the second law of thermodynamics and something called the fluctuation-dissipation theorem. You see, Albert Einstein was good at basically every field of science, and he had something to say about thermodynamics and statistical mechanics; roughly speaking, the movement of energy throughout large physical systems. He knew that the properties of a gas (temperature, pressure, volume etc) were actually measures of the statistical properties of the entire collection of molecules that make up that gas. Further, he was able to show that the processes that lead to individual gas particles randomly losing energy and gaining energy were actually the same process! Can you see how this metaphor applies to our model of human economics?

This was the key. Gas particles don’t care about which of them has more energy when they collide. They don’t sit around working out how much energy each particle can “afford” to lose in an exchange, they just swap pseudo-random amounts of energy, and the result of that process is a stable gas with so-called “equilibrium” properties: constant temperature, pressure, volume, and so on. So a single gas particle with lots of energy might just randomly lose all its energy just due to a few rough collisions, and similarly, a single gas particle with almost no energy might get crashed into from behind and all of a sudden gain a massive amount of additional energy.

But we humans are, in fact, not simple gas particles. We have concepts of justice, ethics and fairness at the microscale as well as the macroscale. Further, on a purely practical level we can’t just swap random amounts of money with one another, that would be chaos. We wouldn’t be able to make decisions properly; a person rich one day would be poor the next for no reason at all. More abstractly, we’d lose some of our individuality and freedom. Nevertheless, we still have to overcome that systemic tendency towards exponential growth, that tendency for one person to suck up all the money. Can we do this and still retain some form of order or the microscale? The answer is yes, by using proportional exchanges.

Proportional Equality

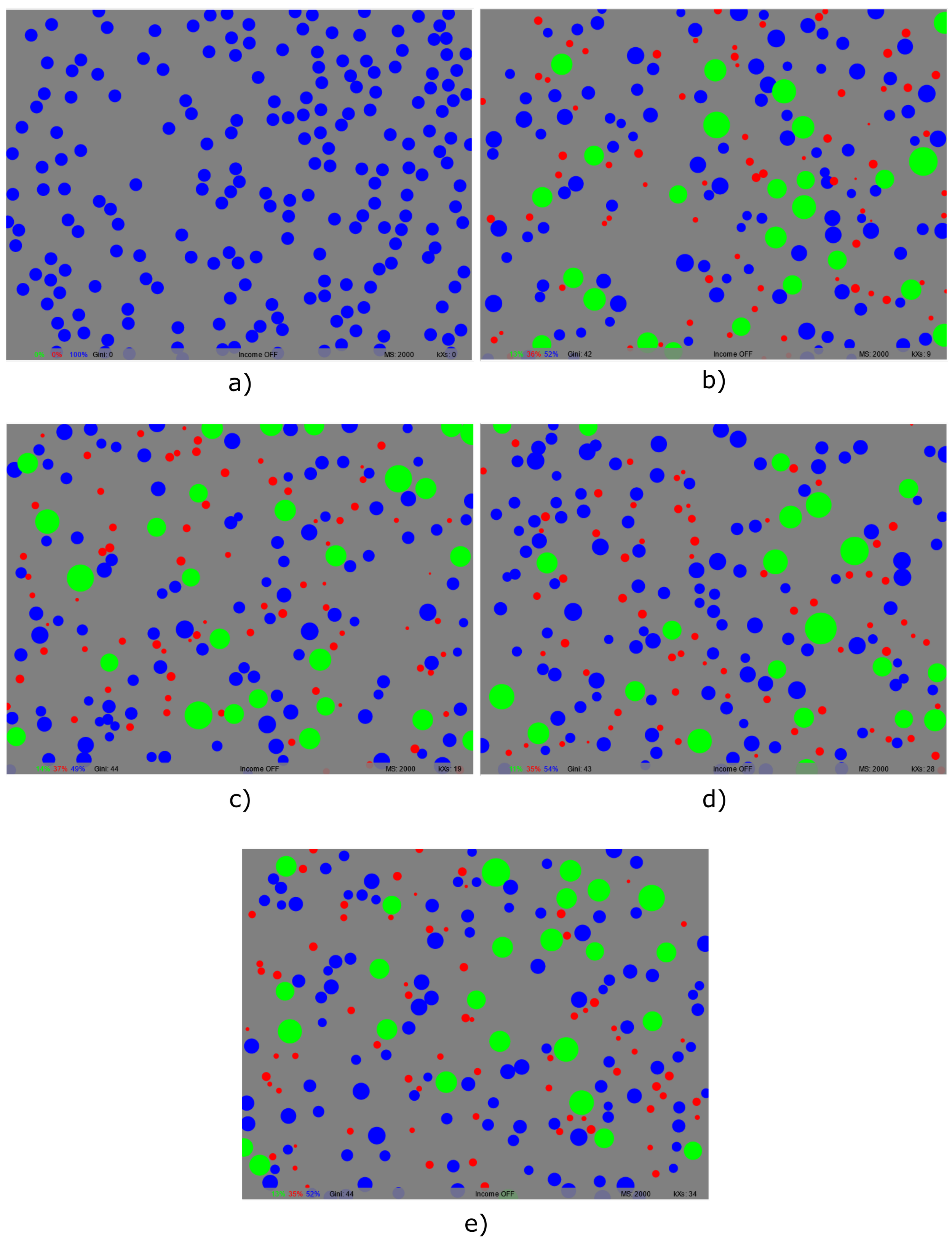
Imagine again that I have £10 and you have £100. Now when we exchange, imagine that when you give me £10, I only give you £1 back. Is that fair? Naively it seems not, but consider, you’ve given me 10% of your value, and I’ve given you 10% of mine. On some level this is fair, on the assumption that we each equally value the same proportion of our wealth. To most people this seems absurd. How can £1 and £10 be worth the same? Or £100 even, £1,000? £1,000,000? Yet this only seems absurd because most of us still live relatively near to the subsistence level, and so our perception of value is what it can buy for us in absolute terms. Yet for the problem characters, the ultra-rich, this is not how money is viewed. Say you own enough money to begin investing seriously in stocks. They don’t talk about absolute return values, do they? They talk about percentage returns, 5% return on your initial investment, for example. Interest rates are similar, as are taxes. When we start talking about the big money, proportionality is what matters and in fact, this may itself be a problem with the system. But given that this is how the economy currently works, why shouldn’t we use the proportion of wealth as the fundamental unit of trade? The rich all do, and the result of that, given a system premised on trades of absolute value, is that the rich get richer and richer with seemingly no end, and the poor get poorer. So instead, let’s seriously imagine that an amount we have exchanged is equal, and a trade “fair”, if the relative proportion of value to the total amount we own is equal. Again, to emphasise the point, the assumption of fairness here is that I value 10% of my wealth as much as you value 10% of yours. Thus there is no “absolute” value of wealth, only proportional wealth. So I made some changes to Philip Rosedale’s code, and if we implement this new proportional trading rule in our simulation and run it, something very different emerges (see Figure 2). You can play with it here[7].

Figure 2: Proportional trades lead naturally to stable distributions of wealth where each individual fluctuates around an average value. The size of each circle represents its associated wealth. Time progresses from a) through to e)

In this case, we get a much more stable distribution. Some people a bit richer, some a bit poorer, but they are all fluctuating around some average value. And we now have a well-defined middle class, social mobility, all the goals of a healthy economy emerging naturally from a set of underlying rules. This is just like the particles of our gas (qualitatively speaking), yet we’ve done it without having to introduce randomness into the system. We still have well defined rules and predictable behaviour, we just had to have change what we mean by a “fair” trade. This concept of fairness, so-called “equal opportunities” vs “equal outcomes” on an individual and societal level is absolutely everything to do with modern politics.

Conclusion

What appears to be fair at the individual level can have profoundly disastrous results at the macroscale, and what appears (perhaps naively) to be unfair at the microscale gives a nice macroscale distribution. Of course human economics is a little bit more complex but the metaphor is clear. Bezos, Musk, Zuckerberg and Co. are not “deserving” of the wealth they own in the meritocratic sense of the word. They are just the lucky ones who are now benefiting from the final stages of an abstract process, a system with rules that cannot help but continue to give them money. We are not in a meritocracy; despite what politicians will tell you, we are in a financial oligarchy and the reason is partially to do with the very notion of a fair trade.

So don't write something off as unfair or ridiculous just because it feels wrong. We didn't evolve to deal with a planet of billions so what “feels” intuitively right for individuals and small little groups may very well be the wrong way to think about it at the global scale. Have a think about proportional trading, but if that doesn’t float your boat, give universal basic income and progressive tax distribution a chance. Then we can properly take back control :)

Bibliography

[1] Rosedale, Philip. “Why do the rich get richer?”. 27/01/2021. Date Accessed: 29/04/2022. https://philiprosedale.substack.com/p/why-do-the-rich-get-richer

[2] Rosedale, Philip. “Why do the rich get richer?” Simulation. 27/01/2021. Date Accessed: 29/04/2022. https://editor.p5js.org/PhilipRosedale/sketches/gcROZDTSV

[3] Piketty, T. (2020). “Capital in the 21st Century”. Harvard University Press. ISBN:9780674979857

[4] Liberal Party of Canada. Date Accessed: 29/04/2022. https://liberal.ca/help-the-middle-class/

[5] Huber, Joel et al. (1982). "Adding Asymmetrically Dominated Alternatives: Violations of Regularity and the Similarity Hypothesis". Journal of Consumer Research. 9(1), 90-98.

[6] Brown, D. (2016). “Happy: Why More or Less Everything is Absolutely Fine”. Corgi. ISBN: 9780552172356

[7] Hanson, Benjamin S. “Why do the rich get richer?” Simulation modification. 27/01/2021. Date Accessed: 29/04/2022. https://editor.p5js.org/benTriesToCode/sketches/q6bj+T8fzT