What is Science? Part 1: The Scientific Method
“We have said throughout this pandemic that we must and we will be guided by the science. When the science changes, we must change our response.”[1]
- UK Prime Minister Boris Johnson on the Covid-19 Pandemic
This statement is a beautiful demostration of Science as it exists in the world today. We’ll get to why that is shortly, but first, what do you think of when you think about “science”? Take a few seconds to think before you continue reading :)
.
.
.
Perhaps you think about experiments being performed in a lab? People in lab coats? Einstein in front of a board of complex-looking maths and sticking his tongue out? A mad scientist from your favourite tv show/movie/book/comic/videogame maniacally laughing? Brian Cox? David Attenborough? Until I started working as a professional scientist I would’ve agreed with you. Now, though, having been a PhD student for 4 years and a post-doctoral researcher for 3 years, I can’t help but see the set of political, economic & social choices and lucky breaks that enable myself and others to perform and share their science. So while I use a lower case “s” to describe science as it is performed, some explicit collection of data, analysis and results, I use a capital “S” to describe Science as a socio-political institution, comprising not only the performance of the scientific method but the people who perform it, the people who fund it, the economics and politics of what science is done and why, the ethics and philosophies of all involved.
So why does the above quote exemplify this instution of Science? Boris, and by extension his government, show an understanding of the technicalities of the scientific method here. He correctly affirms that “the science” changes over time, implying that “science” is a verb, not a noun. He recognises that the acquisition of knowledge ought to change your response to a problem (a statement I wouldn’t usually associate with conservative politics), showing that decisions should be made on a foundation of scientific understanding. However, he specifically uses the term “guided by the science” rather than something stronger like “led by the science“ or “governed by the science“ so as to leave himself the possibility of completely ignoring the scientific results and consensus if he so chooses; likely for political and economic reasons[2], showing that science is embedded within a political framework, not the other way around.
This first post will discuss the scientific method in isolation and how it works from a intuitive perspective. A follow-up Part 2 post will discuss the underlying mathematics that enable science to proceed and the philosophical assumptions we make when doing so. Finally, Part 3 will discuss the external environment which, while enabling science to be objectively performed in isolation, brings the objectivity of the larger institution of Science into serious doubt.
The Scientific Method
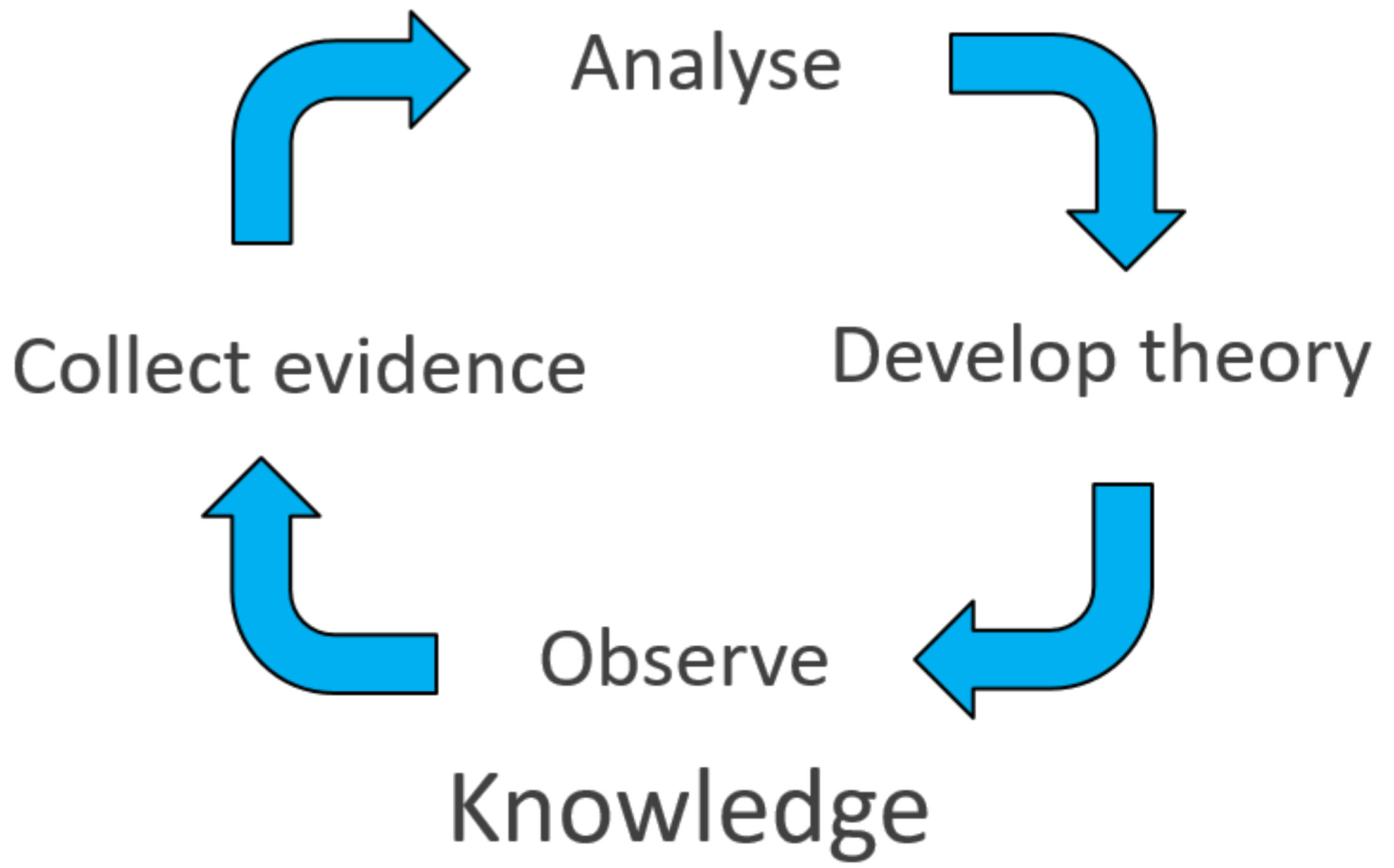
Luckily for us, the simple overview of the scientific method we get taught in school is a really good starting point for understanding how it works (see Figure 1). Before that though, we need a working definition of science. I’m going to use the following
science (verb): A method of using empirical measurements and data to infer general mathematical rules to describe the universe around us and predict its evolution over time.
For completeness, by “empirical measurements”, I mean things that can be observed and experienced from the world around us using either our own senses or more accurate equipment. I also use the term “universe” to mean the set of all data we potentially have access to. So, now we have this definition, how does it work? Let’s do a hypothetical example.
Figure 1: A representation of the scientific method. A key insight here is that it’s a neverending cycle. Knowlege grows as well observe more evidence but is never complete; uncertainty in our theory decreases but is never fully eliminated.
Discovering how trees grow
Imagine you’re out one day and you pass by a huge tree. It’s a sunny day, and you notice that all of the leaves have their flat side facing the sun. The smaller trees around it seem to be getting less of the sun. You may think to yourself that the more light a tree gets, the taller it grows. But how can you go about invesitgating that claim scientifically?
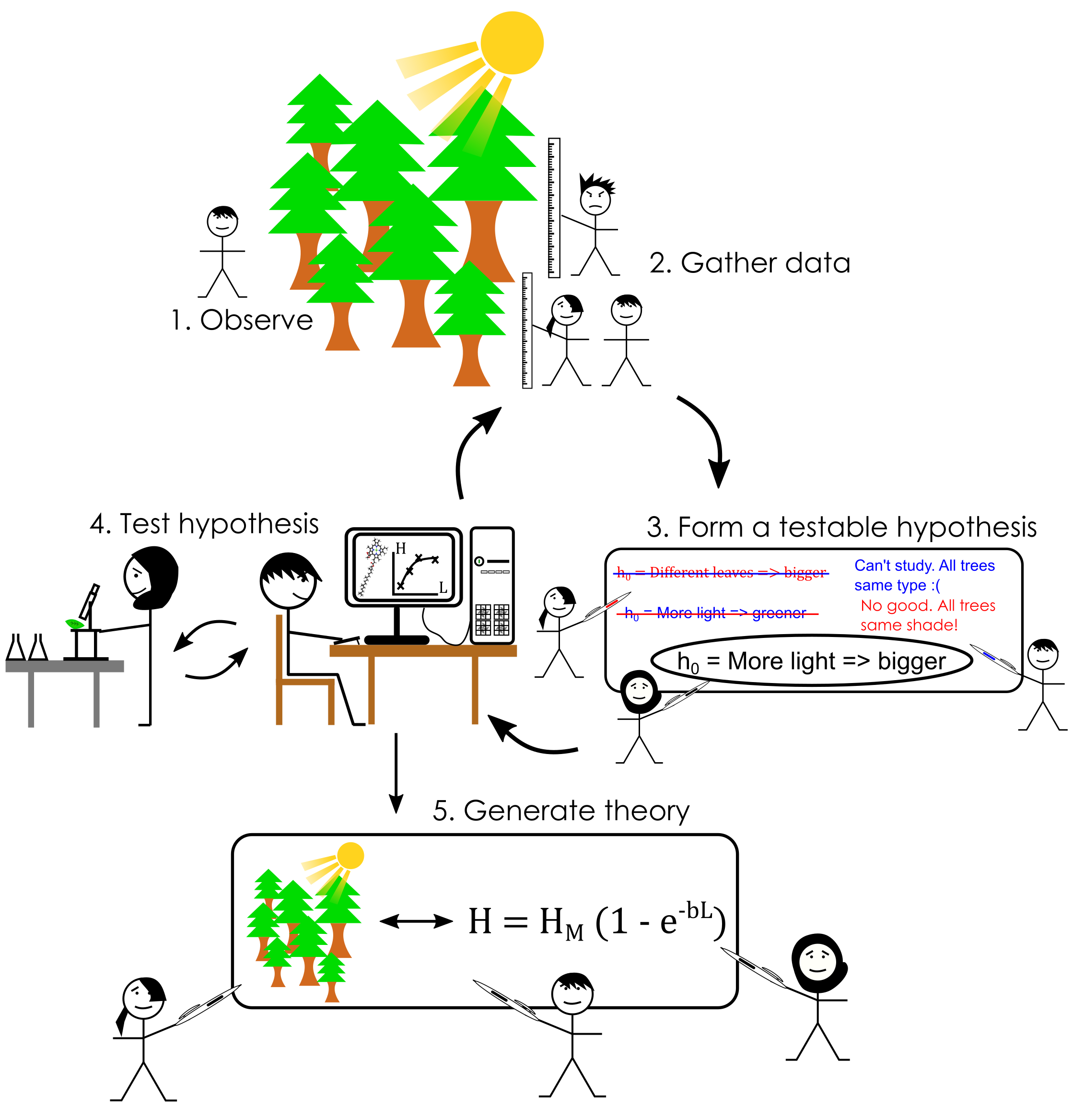
Figure 2 is shows a slight modification of the cycle in Figure 1 and it’s application to the problem of tree growth, so keep an eye on it as we go through.
1. Observe. We already did this, so now we move onto…
2. Gather data. But what data do we gather? It depends on what you’re interested in, but in our case we definitely want to measure the heights of the trees. We also need a way to measure the amount of light a tree gets. A simple way of doing this would be to simply count the number of leaves the tree has. A more accurate way would be to take the shade into account, perhaps only counting the leaves which are fully exposed to the sun. There are a multitude of ever more complex ways to measure light exposure, but we can pick any we like and still use the scientific method to determine whether there is link between them, and what that link is. To move forward we simply need a set of pairs of data points, heights and associated light exposure values. The only difference is that the more accurate your input data, the more accurate your conclusions will be.
3. Form a testable hypothesis. Our testable hypothesis may begin as something colloqial, linguistic and rough such as “the more light a tree gets, the taller it grows”, but we can’t progress with this. There are many ways to have “more light means bigger trees“. Perhaps if we double the amount of light we double the heights of trees? Maybe doubling the light exposure adds exactly 10cm on each time for some reason. Maybe the height vs light relationship changes as we increase the light exposure. “More light means bigger trees“, language in general, simply isn’t specific enough. To proceed in a continuous, logical and specific manner, science requires quantification i.e. mathematics. As such, our “testable hypothesis” will likely be an equation of some form. If the height of a tree is denoted H and the amount of light L, then our testable hypothesis may be something like
which is an equation for a straight line. If m = 2, say, this would represent our “double light => double height“ example. But how do we test whether this is true?
4. Test hypothesis. Statistical analysis allows us to use of all the pairs of tree heights and light exposures to determine how good of a mathematical model this is. We likely need to do further analysis in the lab or via computation to properly investigate our variables, but once we have them, we can use a technique called “statistical regression analysis“ to investigate how well some equation relates two variables. Generally speaking, it is the goal of the scientific method (when applied to a specific problem) to determine some equation that relates two variables as accurately as possible. But there is a very good chance that our initial investigation will not give us what we were looking for at first. Our initial hypothesis may not be accurate enough for our liking, or be completely wrong. We may not have enough data, or we may figure out a way to collect better, more accurate data. Hence, just as in Figure 1, steps Figures 2.2, 2.3 and 2.4 are part of a cycle of increasing accuracy. In principle this cycle is neverending, but in practise we stop once we reach a certain level of accuracy. Figure 2.4 actually shows an experimentalist and a theoretician working together to extract chlorophyll from a leaf and use it to better quantify the light exposure. On the computer screen, we see a reasonably accurate “fit” to the data points using regression analysis. If this were to happen, we would be able to…
5. Generate Theory. If we have an equation that fits our data well then that’s great! But it isn’t a theory just yet. More often than not, equations that fit data well are not pulled out of thin air. They are mathematically generated from more fundamental equations, and so each of our variables has some underlying physical meaning already. Technically speaking, the process of using statistics to infer how two variables relate to one another is called inductive reasoning, whereas the process of using analytical mathematics (and to some extent computer simulations) to derive new equations is called deductive reasoning. The scientific method brings these two forms of reasoning together to meet in the middle, and only if we meet in the middle can we say we have a theory. Any piece of mathematics used in scientific theories ought to be both deducable from fundamental principles, and also measurable via some experiment. The reason we need both to meet in the middle is an extremely philosophical problem so I’m not getting into that here. This is simply a description of how science works in practise!
I emphasise that I made this up for an example. This is probably not how trees grow. It might be! But it might not. I was aiming to be somewhat intuitive (we’ve all noticed that trees grow in sunlight before, right?), but in reality, the biophysics of how trees grow is insanely complex. So many more things than the amount of light affect plant growth, such as soil quality (whatever that means), density of folliage, temperature etc. I gave a simple equation with a single variable (L) as an example, but that’s just an example. If you’re interested in this specific science, do some research into it :)
Figure 2: The scientific method in practise, with angry PhD students included for realism! Experiments, calculations and computer simulations are performed in parallel, one after the other, in the same research group, and between competing research groups. All of this is cobbled together through scientific publications and conferences so that the cycles shown here and in Figure 1 still work.
Conclusions
We’ve seen that the scientific method is a cycle, and with each cycle we update the probability of our initial hypothesis being correct. If it is correct (within some level of accuracy), great! If it is not correct, we create another hypothesis and continue the cycle. This process of updating probabilities based on available data, of reducing our uncertainty in our hypotheses, is what science is. Not the technological side-effects, not the economic benefits, but the understanding and interpretation of data. Reducing uncertainty via the scientific method is what many scientists would call “knowledge”, with some going so far as to say that any other form of “knowledge” is simply nonsense. But I’m not going to get in that here! Maybe another day though…
In the next post we’ll see how the scientific method can be represented mathematically, and what this means for scientific understanding changing over time. Stay tuned!
Bibliography
[1] Johnson, Boris (2020), The Prime Minister’s Statement on Coronavirus in Full, Conservative Party, Date Published: 19th December 2020, https://www.conservatives.com/news/tier-4-announcement-speech, Date Accessed: 25th April 2021
[2] Hayward, Freddie (2021), Why Boris Johnson can’t claim to have “followed the science” on Covid-19, New Statesman, Date Published: 2nd February 2021, https://www.newstatesman.com/politics/uk/2021/02/why-boris-johnson-can-t-claim-have-followed-science-covid-19, Date Accessed: 25th April 2021